a cura del prof. Spadari Amedeo
Si usa la prova del 9 per controllare l'esatezza di una
moltiplicazione tra numeri relativamente grandi quando i calcoli sono fatti a
mano.
Se nella prova l' esito è negativo i calcoli sono sbagliati ed occorre rivederli
nella moltiplicazione,se l' esito è positivo il risultato è corretto a
meno di un multiplo di 9.
Pochè sbagliare di un multiplo di 9 una moltiplicazione è abbastanza difficile,
si può dire che la prova torna ed il risultato calcolato sia corretto.
1. Procedura
1.1 per le moltiplicazioni
1.2 per le divisioni intere
1.3 per le divisioni con resto
2. Significato prova del nove
Classi di resto modulo 9
3. Il perché proprio del 9
Proprietà del numero 9 nel nostro sistema di numerazione posizionale decimale
1.1 Come si procede nel calcolo della
prova del 9 per le moltiplicazioni
Esempio
54.178 x 123.456 = 6.68.599.168
Il risultato sarà corretto? Si esegua la prova del 9.
Si tracci una croce e si mettamo i seguenti numeri interi ad una cifra:
in alto a sinistra: del primo fattore si sommino le cifre
(5+4+1+7+8=25=(2+5=7) cioè fino a quando non resta un numero ad una sola
cifra
| 7 | |
in alto a destra analogamente si faccia lo stesso procedimento con il secondo
fattore (1+2+3+4+5+6=21 =2+1=3)
| 7 | 3 |
n basso a sinistra: si moltiplicano i 2 numeri in alto sulla
croce e si riduce il risultato ad una sola cifra, (7 x 3 =21= 2+1=3)
| 7 | 3 |
| 3 |
Infine in basso a destra si metta la somma del risultato
dell'operazione (6+6+8+8+5+9+9+1+6+8=12 4+2=3)
| 7 | 3 |
| 3 | 3 |
Se i due numeri in basso sono uguali la prova ha esito positivo, altrimenti ha esito negativo.
N.B.
Se la prova è negativa la moltiplicazione è per certo sbagliata, mentre se è
positiva il risultato trovato potrebbe essere corretto oppure differire
per un multiplo di 9.
| Somma cifre primo fattore |
Somma cifre secondo fattore |
| Somma cifre prodotto dei 2 numeri in alto |
Somma cifre risultato |
1.2 Calcolo della prova del 9 per le
divisioni intere
Dal momento che dividendo : divisore = quoziente
Segue che divisore x quoziente = dividendo
Per cui abbiamo:
| Somma cifre divisore |
Somma cifre quoziente |
| Somma cifre prodotto dei 2 numeri in alto |
Somma cifre dividendo |
1.3 Calcolo della prova del 9 per le
divisioni con resto
Dal momento che dividendo : divisore = quoziente con resto non 0
Segue che divisore x quoziente + resto = dividendo
Per cui abbiamo:
| Somma cifre divisore |
Somma cifre quoziente |
| Somma cifre prodotto dei 2 numeri in alto + somma cifre resto |
Somma cifre dividendo |
Esempio
865 : 21 = 41 con resto 4
| 21 2+1 3 |
41 4+1 5 |
| 3x5=15 1+5=6 Dunque 6 è la somma delle cifre del prodotto tra i 2 numeri in alto; a questa bisogna aggiungere il resto (4), per cui risulta 6+4=10 = 1
|
8+6+5=19 1+9=10
1 |
Significato prova del 9 in particolare per le moltiplicazioni
Quando si fa la prova del 9 occorre basarsi sulle "classi di resto".
Normalmente i numeri interi positivi si studiano disposti su una semiretta
orientata.
Si ha dunque una situazione del tipo:
|----|-----|-----|-----|----|-----|-----|-----|-----|----|-----|------|---------->
0.. 1... 2.... 3.... 4.... 5... 6... 7.... 8.... 9.. 10.. 11.. 12 ...
Alcune semplici considerazioni a mò di chiarimento
Posizionando invece i numeri a mò di orologio con nove segni
0,1,2,3,4,5,6,7,8
si avrà una situazione del tipo:

Che cosa si ha nei cerchi dei varie segni?
Nel cerchio del segno dello 0 si ha all'inizio 0 ,poi dopo il primo giro 9,dopo
il secondo giro 18 e via dicendo ...
Nel cerchio del segno dello 1 si ha all'inizio 1 ,poi dopo il primo giro 10,dopo
il secondo giro 19 e via dicendo ...
Nel cerchio del segno dello 0 si ha all'inizio 2 ,poi dopo il primo giro 11,dopo
il secondo giro 20 e via dicendo ...
.
.
.
Nel cerchio del segno dello 8 si ha all'inizio 8 ,poi dopo il
primo giro 17,dopo il secondo giro 26 e via dicendo ...
Nel cerchio del segno dello 1 ci sono tutti i numeri che divisi per 9 danno
resto 1 ( tornerà utile per la divisione).
Nel cerchio del segno dello 2 ci sono tutti i numeri che divisi per 9 danno
resto 2 ( tornerà utile per la divisione).
E così via.
Presa un cerchio a caso e presi 2 numeri a caso da esso, la differenza
tra questi 2 numeri è sempre un multiplo di 9.
Presa un cerchio a caso e preso a caso un numero, la somma delle sue
cifre è il numero rappresentante del cerchio eccetto il cerchio dello 0 nel
quale tutti i numeri (0 escluso) danno per somma 9.
Applichiamo queste considerazioni all'addizione.
Come si fa 4+2 sulla semiretta?
Si parte dall'origine e si cammina di tanti passi quanto indicati dal primo
addendo; poi ci si muove ancora del numero di passi indicati dal secondo
addendo. Alla fine ci si ferma, alziamo gli occhi sul "cartello" che ci indica
(in buona sostanza) quanti passi ci siamo allontanati dall'origine cioè 6 passi.
|----|-----|-----|-----|----|-----|-----|-----|-----|----|-----|------|---------->
0 .......................4...|
...............................|----2----|
Analogamente anche nel modo di rappresentazione dell'orologio si parte
dall'origine (cerchio dello 0), si fanno 4 passi in senso orario e poi altri 2 e
anche qui vediamo che si sono fatti 6 passi dall'origine.
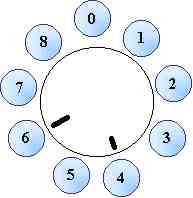
Proviamo con 8 + 6
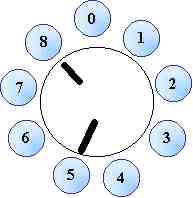
Dunque 8+6= 14 = 5
In realtà si sono fatti un giro ( una novina ) + 5 passi
dall'origine.
Si osserva immediatamente che sommando ripetutamente le cifre di un numero
nel nostro sistema di numerazione decimale , fino a ridurlo ad un numero
di una cifra soltanto, si ottiene il resto di quel
numero nella sua divisione per 9
N.B. il numero è dato dal numero di giri x 9 + il resto
Deduzione per le divisioni
Con la prova del 9 si calcola il resto della divisione per 9 del primo fattore, il resto della divisione per 9 del secondo fattore, moltiplichiamo questi 2 numeri e sommando le cifre del risultato, si ottiene il resto della divisione per 9 che il risultato corretto deve avere.
Poi si calcola il resto della divisione per 9 del risultato che si è calcolato.
A questo punto se questi 2 numeri sono diversi, la divisione è errata, mentre se i numeri sono uguali, la divisione è corretta a menodi 9, ovvero differiscono tra loro per un multiplo di 9.
Il perché proprio del 9
N.B. Si è visto che la somma delle cifre di un qualsiasi numero dia
come risultato il suo resto nella divisione per 9.
Ciò avviene perché nel nostro sistema di numerazione è decimale posizionale, 9 è il maggiore tra i numeri che si possono scrivere con una cifra soltanto.
Si osservi che la divisione di 10 per 9 dà resto 1 (10=9+1 e 9 è divisibile per
9)
Analogamente la divisione di 100 per 9 (100=99+1 e 99 è divisibile per 9), di 1000 per 9 (1000=999+1), e così via.
La somma delle cifre di 10, 100, 1000, è sempre 1.
Ma anche che 20, 200, 2000, ecc, hanno resto 2 nella divisione per 9.
Anche per 30, 300, 3000.
Dato un qualunque numero, è possibile determinare il suo resto
nella divisione per 9 semplicemente sommando le sue cifre.
La prova del 9 è molto semplice determinare il resto della
divisione di un numero per 9 (basta sommare le sue cifre ripetutamente finché
non resta un numero ad una sola cifra), in più "sbagliare" di un multiplo di 9 è
cosa abbastanza rara ed è chiaramente pratica nel sistema di numerazione
posizionale decimale.
N.B. La prova dell' 6 o dell' 8 è ugualmente fattibile nei sistemi di numerazione esadecimale e ottale , a Voi provare.